1. Introduction

The conundrum of wave-particle duality has long been reported in even the most elementary of texts (see e.g. [1]). Wavelike properties are required to account for several phenomena, including optical refraction and neutron diffraction. The simplest case used to demonstrate this behaviour is the double slit experiment, shown in Figure 1.

Figure 1: The double slit experiment. Incident particles pass through the double slit apparatus and are detected as events at the detector.

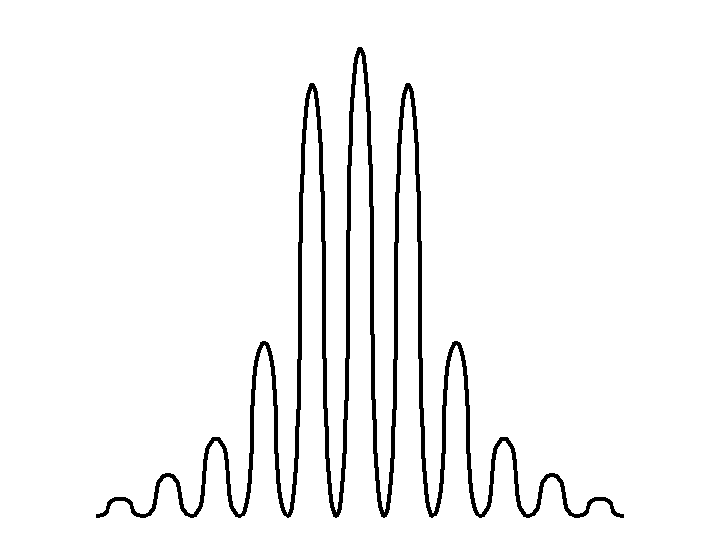
The difficulty has always been associated with the fact that individual particles behave like particles, but the average behaviour of a large number of particles resembles that of a wave. The meaning of the term "particle" used here is defined in Section 3 below. Each particle can be detected at the detector as a discrete event. In the case of a single slit, the average behaviour of a large number of particles appears to be governed by an approximately normal probability distribution. But in the case of double slit, the distribution is modified to produce a modulation effect, as shown in Figure 2.

Figure 2: The apparent modulated waveform at the detector when the effects of a large number of particles passing through the double slit apparatus are summed together.

The question arises, how can independent particles, each of which is recorded as a discrete event at the detector, somehow collaborate to form a wavelike pattern? Additionally, if an attempt is made to discover through which slit each particle passes, the wavelike effect disappears. This is usually accounted for by citing the Heisenberg uncertainty principle, but without any attempt to explain how the slit measurement interferes with the experiment.

2. The de Broglie vector

We have previously proposed a quantum mechanical property known as the de Broglie vector, r_db [2] to explain how observations in different frames of reference result in different de Broglie frequencies. The de Broglie vector can be considered to be a probability vector of amplitude ħ/mc. The vector rotates as the particle moves, rather like the spin of a neutron in a neutron spin echo experiment [3]. In the case of the spin echo experiment, the direction of the spin axis at the detector determines the probability that the neutron will be detected as spin up. If the spin axis is parallel to the detection axis it will be detected with a probability of 1, whereas if it is anti-parallel, the probability of detection will be zero. In the case of the de Broglie vector, the vector is assumed to rotate with de Broglie frequency, f_db, according to the equation:

f_db =	mv²		1
	h

with no requirement for a magnetic field. The de Broglie vector is sufficient to completely describe interactions with other bodies, such as when the particle is detected by a double slit apparatus.

3. The nature of a quantum particle

It is assumed that a quantum particle can be represented by nothing more than the de Broglie vector and a probability function in space. For the purpose of the double slit experiment, it is sufficient to reduce the probability function to a single dimension, as shown in Figure 3.

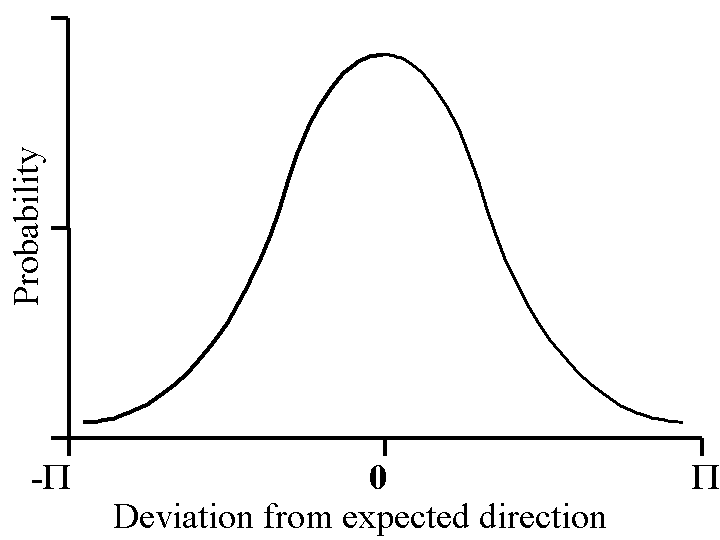
Figure 3: A particle expressed as a directional probability function, viewed from the last point of detection. Using quantum mechanical principles, its source can be regarded as the last point of detection.

The probability function can be regarded as a radial distribution with the origin as the last point of detection. The source of a particle will be regarded as the last point of detection for the purpose of this analysis. Thus when the particle encounters a double slit apparatus, if it is transmitted, a new probability function is defined with its origin at the double slit.

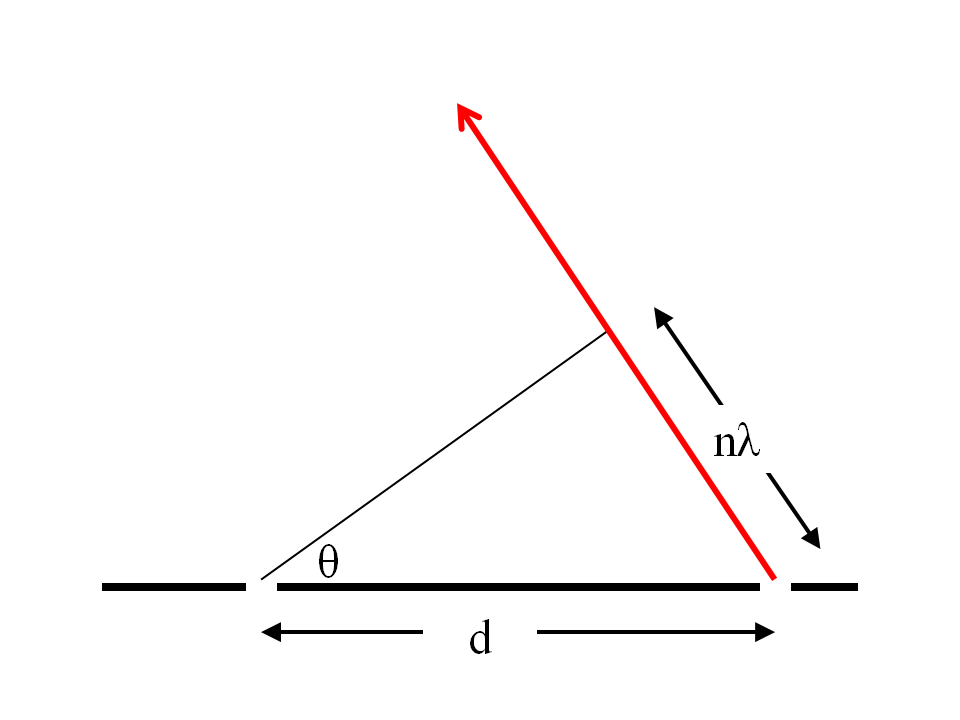
4. The double slit experiment explained

Figure 4: The geometry of the double slit experiment

In Figure 4, d is the separation between the slits, θ is the angle of deflection, n is a non-negative integer and λ is the de Broglie wavelength of the quantum particle. In order to explain the double slit experiment in purely quantum mechanical terms it is necessary to abandon the idea that a particle passes through only one slit. The double slit apparatus only detects the particle on the scale of the double slit and hence this is the scale to which the probability function can be said to collapse. Now the particle may reach the detector at any point defined by a new probability function (see Figure 3). However, at an angle θ, such that:

nλ =

d sin θ

the de Broglie vector from the two slits will be in phase. In this case the particle will be transmitted with a probability of 1. On the other hand, if

(2n + 1)λ =

2d sin θ

the de Broglie vector from the two slits will be anti-phase and the particle will be transmitted with a probability of 0. In other words, it will either be absorbed or reflected by the double slit apparatus. At all other values of θ, the probability of transmission will be intermediate between 0 and 1. The closer it is to satisfying Equation 2 the greater the probability of transmission. The closer it is to satisfying Equation 3 the less the probability of transmission. By convoluting the probability of Figure 3 with the probabiltity defined by the de Broglie vector we arrive at Figure 2.

5. How detecting the slit interferes with the experiment

Detecting the slit through which the particle passes reduces the scale of detecting to that of a single slit. Hence a detected particle will have its directional probability collapsed to a single slit and therefore the de Broglie vector will have only a single component. Thus the distribution at the detector will be reduced to that of Figure 3.

6. Conclusions

A mechanism has been proposed to describe the double slit experiment in entirely quantum mechanical terms. This offers a means to dispose of the need for wave-particle duality.

References

[1] R Feynman: The Character of Physical Law, MIT Press (1967)
[2] L D Howe A quantum approach to relativity, www.innovationgame.com/physics (2000) (2000)
[3] F Mezei, Neutron Spin Echo: in the series:- Lecture notes in Physics 128 Springer-Verlag (1979)

Abstract