Logo
Logo
Innovation­game

Refraction of Quantum Particles Without Waves

January 2001

Abstract

This paper describes a possible mechanism for refraction without recourse to wave theory.  It therefore offers a vehicle to eliminate the need for wave-particle duality when describing the behaviour of quantum particles.  The crux of the hypothesis is the postulation that a quantum mechanical particle may be regarded as existing in two places simultaneously.  Using this assumption, it is possible to derive Snell's law solely from the velocities of the quantum particle in the two media.  The derivation is independent of the relative positions of the two positions of the particle.

1.  Introduction

Wave particle duality has been a requisite part of quantum mechanics since its inception.  In particular, it is required to explain the wavelike behaviour of quantum particles during diffraction and refraction.  This paper is intended to offer a non-wave dependent description of the refraction process.  We have previously proposed the De Broglie vector as a means of describing a quantum particle  [1].  The De Broglie vector has been further used as a means to describe the diffraction process in a double slit experiment  [2]. 

2.  Analysis

The De Broglie vector approach to the double slit experiment assumes that a quantum particle can pass through both slits simultaneously.  Such behaviour may be attributed to the rotation of the de Broglie vector given by the formula:

fdb  =  mv2  1
h

If the axis of rotation is coincident with the velocity vector, the quantum particle can be represented as two particles, one at each extremity of rotation of the de Broglie vector.  The simplest method of treating this model is to imagine that a quantum particle actually exists as two particles, such as Pa and Pb in Figure 1. 


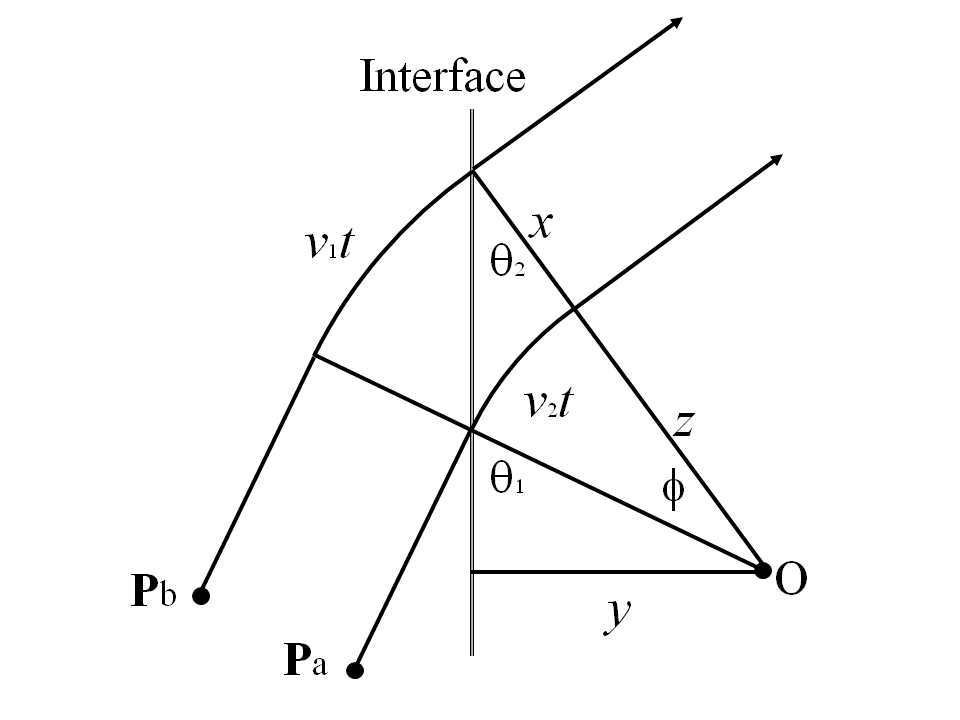
Figure 1: A two particle visualisation of refraction.  If two particles travel with a constant separation, x, they will describe a curved path at the refraction interface, which satisfies Snell's law.

We use the following argument to show that the quantum particle will satisfy Snell's law.  Assume that the separation between the particles is some arbitrary distance x and the speeds of the particles in the incident and emergent media are v1 and v2 respectively.  When Pa crosses the interface, its speed will be reduced to v2, whereas Pb will continue to travel at v1 until it reaches the interface.  If the particles continue with a separation of x, they will describe the curved path around the point O, as shown in Figure 1.  After Pb crosses the interface they will travel in a straight line once again.  If Pb reaches the interface t seconds after Pa, it can be seen that

v1t  =  φ (x + z)  2

and

v2t  =  φ z  3

hence

  φ = v1 = v2  4
t x + z z

so

  v1 = x + z  5
v2 z

Now

Sinθ1  =  y  6
z

and

Sinθ2  =  y  7
x + z

so

  Sinθ1 = x + z  8
Sinθ2 z

From 5 and 8

  Sinθ1 = V1  Q.E.D.
Sinθ2 V2

3.  Conclusions

The analysis is completely independent of x, the inter-particle separation, which is effectively twice the amplitude of the de Broglie vector.  Thus, it can be demonstrated that any quantum particle will obey Snell's law, without recourse to wave-particle duality. 

References

[1] L D Howe A quantum approach to relativity, www.innovationgame.com/physics (2000)
[2] L D Howe A Possible Mechanism for Wavelike Observations of Quantum Particles, www.innovationgame.com/physics (2001)